简介
这次的课程视频中主要讲了神经网络的构成，和在神经网络下的 BP 算法。整体为接下来的作业打好了基础，视频的最后也给出了对一个项目研究的基本步骤。
分类问题 - 逻辑回归的拓展
这部分为了让我们在接下来能够看的更顺利一点，做了一些名词解释：
- ${x^{(i)},y^(i)}^N_{i=1}$
- $x_i$：输入，e.g. words (indices or vectors!), context windows, sentences, documents, etc.
- $y_i$：输入的标签向量
- $\mathcal{R}^{C\ \times\ d}$ ：代表该矩阵是 $C\ \times\ d$的
防止过拟合
这里讲的很浅，只讲了加了一个 L1 正则项，详情可以参考我之前的线性回归章节中对 Ridge 回归和 Lasso 回归的说明，是一样的。还讲了一些过拟合的图如下，老生常谈吧，比较简单：
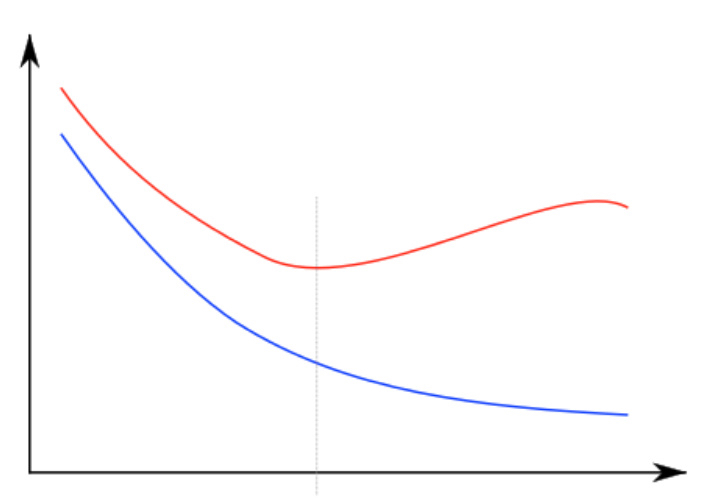其实，一般而言神经网络越复杂，在数据集很小的情况下非常容易过拟合。
The softmax and cross-entropy error
使用交叉熵可以被写为熵和 Kullback-Leibler 距离的形式：
\[H(p,q) = H(p) + D_{KL}(p||q)\]其中 $D_{KL}(p||q)$为如下公式：
\[D_{KL}(p||q) = \sum_{c=1}^C p(c)\log{\frac{p(c)}{q(c)}}\]The KL divergence is not a distance but a non-symmetric measure of the difference between two probability distributions p and q
当然我们的例子中， $H(p)$ 是 0。在我们用的时候它的公式如下：
\[H(p,q) = -\sum_{c=1}^C p(c)log{q(c)}\]其中 $p(c)$ 代表着 c 和其他单词的关系，在我们这里用的是 one-hot 向量，所以只有选定的词的概率会输出。
一些小建议
这些建议是在小数量集的情况下，re-training词向量多次会让模型表达不好，例子如下：
- 在训练集中，训练的向量中
telly,TV，television这三个词在一起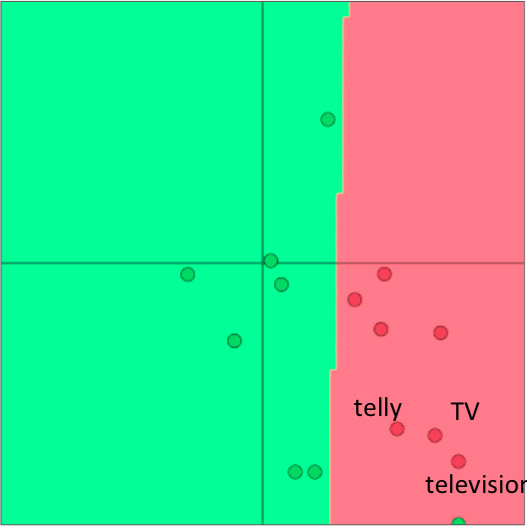
- 如果重新训练，可能
television没有划分在里面，那么训练结果显然就有问题了。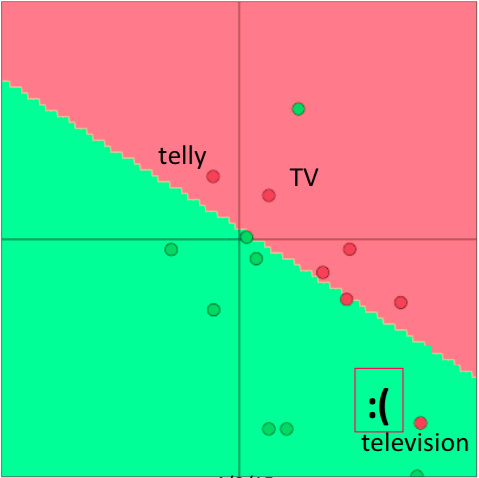
之前我们在 softmax 来表示 $p(y|x)$ 中使用的是 $W_y·x$ 这个公式作为 $exp(f(x))$ 中的 $f(x)$ 。
Window classification
只通过一个单词来判断它的意思是很难做到的。一个单词很可能有多种意思，这些意思甚至是相反的意思。所以我们需要通过上下文，也就是窗口来判断这个单词是什么意思。
也就是说输入的 $X_window$ 是一个词向量拼接而成的，如下：
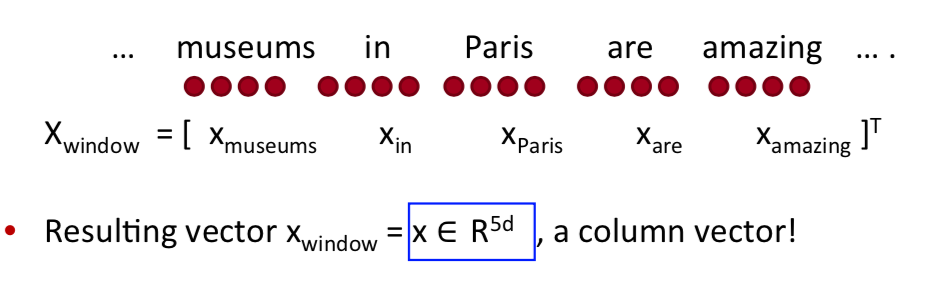这个窗口向量的维度为 $\mathcal R^{5d}$，其输出的 $\hat y$ 为：
它的交叉信息熵如下： \(J(\theta) = \frac{1}{N}\sum_{i=1}^{N} -log(\frac{e^{f_{y_i}}}{\sum_{c=1}^C e^{f_c}})\)
接下来就是 BP 的推导，这部分还是在 Assignment01 的总结里推导这部分公式。这部分就是把一个对一个词向量 BP 的过程扩展成一个矩阵的运算，用矩阵运算编出来的程序会快至少一个数量级。
小建议
- 小心的定义你的变量们，并且一直跟踪他们的维度
- 使用链式法则 (Chain Rules)！
神经网络
从逻辑回归到神经网络，在之前的机器学习的文章中，我提到过集成学习中除了 boost 和 bag 两个策略外还有一个 Slack。我们可以粗浅的理解神经网络是用一堆逻辑回归通过某种策略链接而成的由一堆若分类器构成的集成学习。
接下来就是一些简单的神经网络说明术语：
- neuron：个人的理解就是一个逻辑回归连一个激活函数
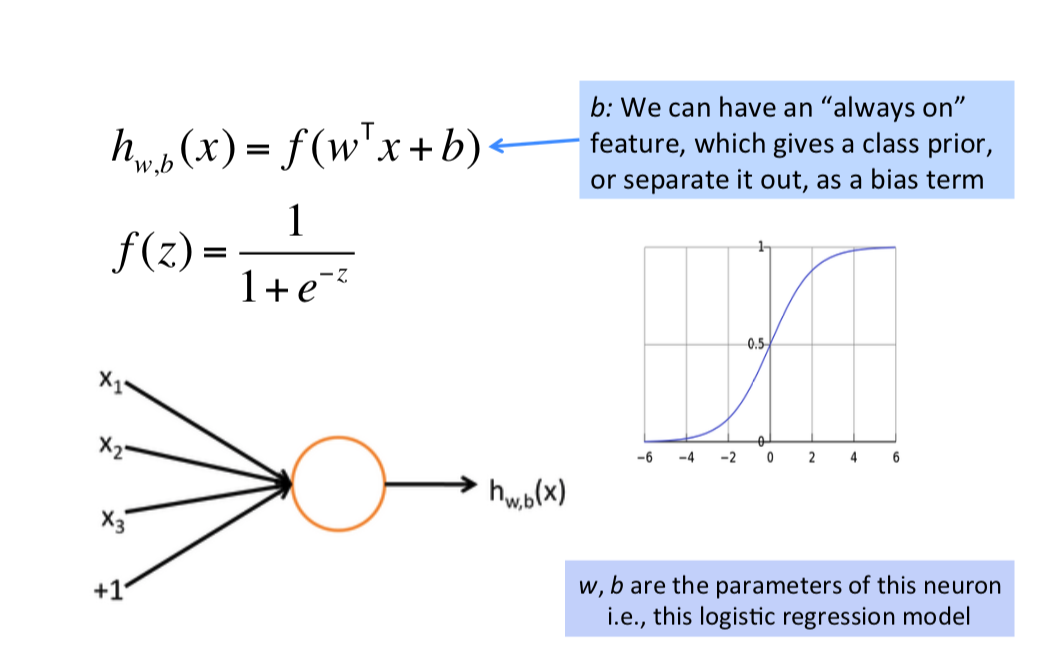
- A neural network：多个逻辑回归的输出，有几个逻辑回归输出下一层就有几个神经元
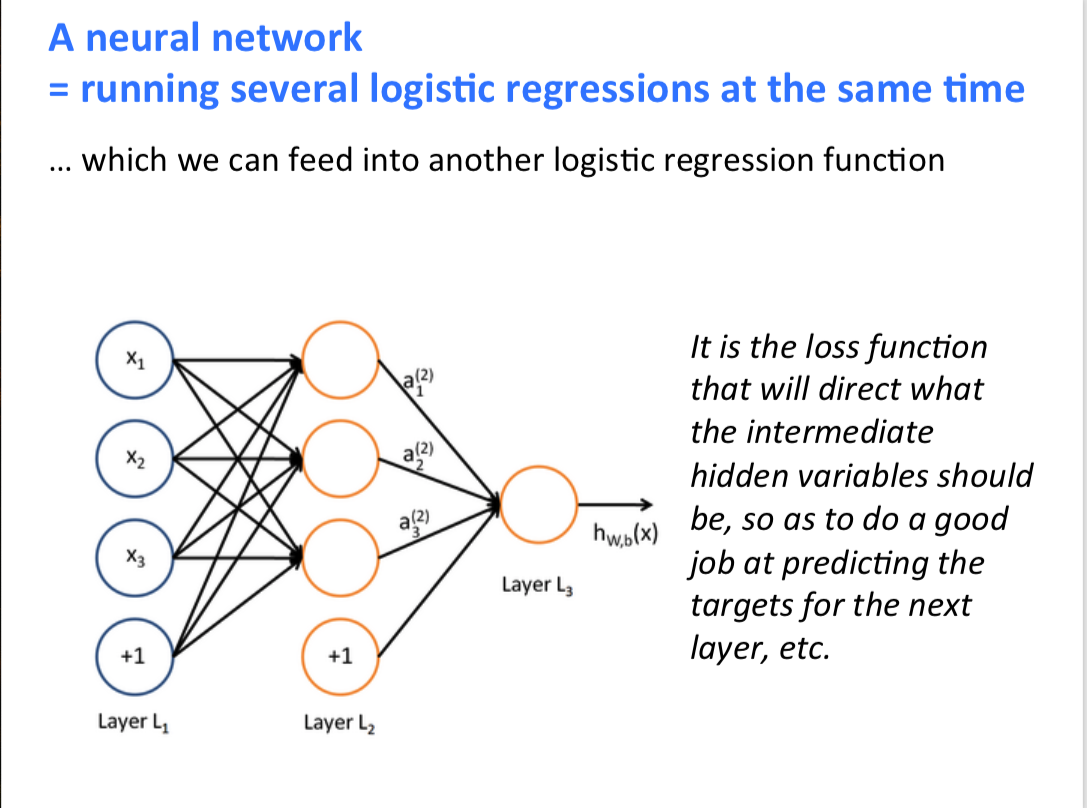
- $score(x)$：得分函数，可以理解为前向传播的结果
一些矩阵方面的说明
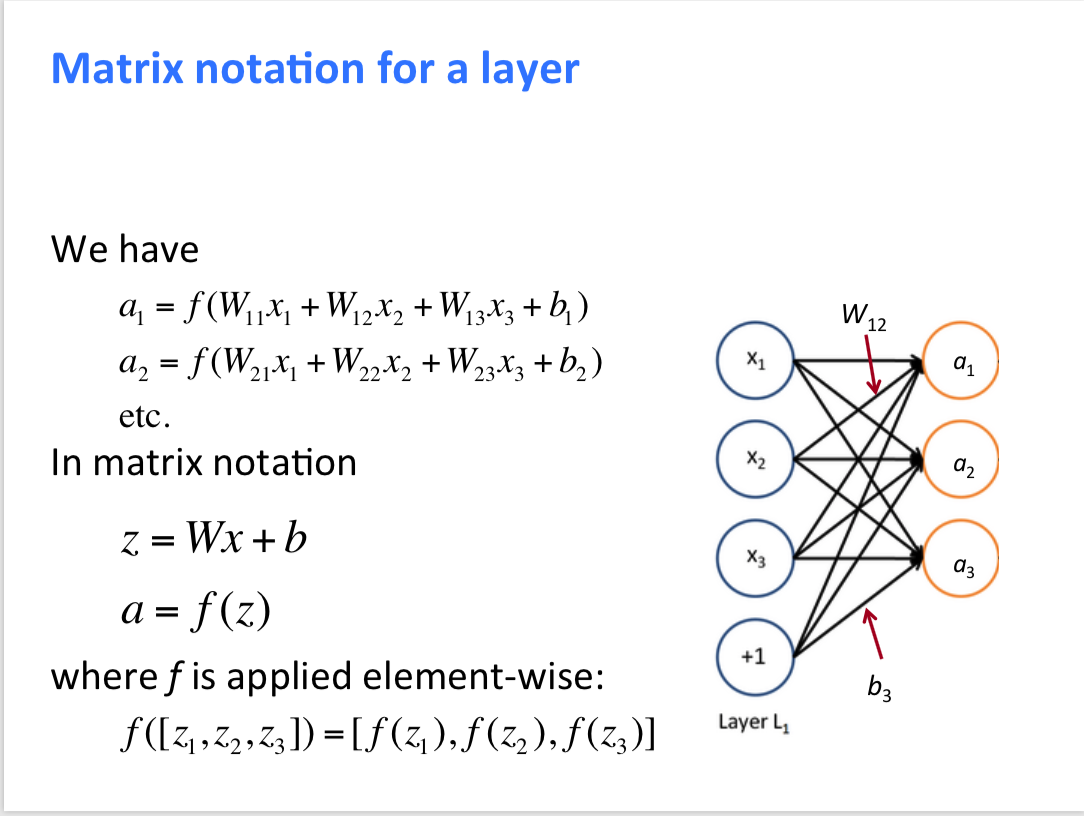可以看到中间层中每一个神经元对应了一个 $W$ 矩阵，图中的一共 3 个 $W$ 。
为什么要激活函数
想想我们逻辑回归是线性的，也就是只能画“直线”解决线性问题，那么出现了非线性的问题怎么办。假设不实用激活函数，结果则是一堆逻辑回归的叠加，即线性层的叠加效果很差。所以使用 sigmoid 函数来将非线性转线性，当然现在用 ReLu 比较多。这样子就能解决非线性问题了。
间隔最大化目标函数
这一部分大佬的博客中有详细的说明，如下我就整段摘抄了：
怎么设计目标函数呢，记 $s_c$ 代表误分类样本的得分， $s$ 表示正确分类样本的得分。则朴素的思路是最大化 $(s - s_c)$ 或最小化 $(s - s_c)$。但有种方法只计算 $s_c > s \Rightarrow (s_c−s)>0 $ 时的错误，也就是说我们只要求正确分类的得分高于错误分类的得分即可，并不要求错误分类的得分多么多么小。这得到间隔最大化目标函数：
这里的逻辑其实是，之前的逻辑回归画的“线”可以有很多条，之前没有规定选哪条最好，现在这个算法就是选一个最好的“线”，将间隔转换为几何间隔，这点和 SVM 很类似，公式中的 1 可以理解为，SVM 中的松弛因子是一个超参，它代表着其中一些点的重视程度，具体可以参考我之前的SVM 的博客中的松弛因子部分的说明。
注：帅小哥说通常 1 的效果比较好
有意思的说明
- 使用矩阵来运算而不是写个
for循环单独对一个个向量运算会快很多。帅小哥的例子中快了 12 倍。所以矩阵是你的朋友，所以尽可能多用他们。
- 在实验中神经网络多出来的那一层（隐含层）的作用，可以理解为是不同输入词之间的非线性作用
- 传统 ML 和神经网络的区别
- 实验的流程（这一波不知道为什么 PPT 中没给）
- Split your dataset：分为训练集80%，验证集10%，测试集10%。其中测试集直到快 deadline 前都不能用。
- Establish a baseline：选一个模型来训练作为你的基准
- Implement existing neural net model
- Always be close to your data：
- 可视化他们
- Collect summart statistics
- 查看模型错误
- 注意超参的影响
- Try out different model variants
- 多选用多种分布的数据集进行比对结果，看看哪些分布没有捕捉到
- 研究的流程
- 早点开始调研看 paper
- 拼直觉（本事）找到现有模型的漏洞
- 和导师聊自己的看法
- 测试自己的想法（但是要小心验证） 简单的来说就是，大胆猜想，谨慎验证，现在行动
- SGD 的一些说法：
- 由于使用 SGD，你不停的在随机更新，这使得你的模型不容易陷入局部最优解，这也是SGD比较快，效果还好的一部分原因。
- 事实上你的窗口越小，你的随机性越大
- 关于 BP 的推导在大佬的文章中有，大家可以自行查看，之后在作业的总结中还会推。