Intro
上一篇我们讲了 MonteCarlo 和 TD 方法,他们都是用于在五模型的时候估算当前各个状态的 Value 的,即已经有了 Policy Evaluation 部分。我们还需要一个 Policy Impovement 的部分。这部分就是来解决这个问题的。在优化控制部分,我们根据是否根据已经拥有他人的经验来更新自身的控制策略,将优化控制分类下面两类:
- Online-policy Learning 其基本思想是个体已经有一个策略,并且根据这个策略去进行采样,并根据使用了这个策略得到的一些行为的奖励,更新状态函数,最后根据更新的价值函数来优化策略得到的最有的策略。
- Offline-policy Learning 其资本思想是个体已经有了一个策略,但是不根据这个策略进行采样,而是根据另一个策略进行采用。这个策略的来源可以是先前学习的策略,也可以是人类给出的策略。在自己的策略形成的价值函数的基础上观察别的策略产生的行为,以达到学习的目的。小帅哥说,这种事类似于“站在别人肩膀后面观察他人行为的一种方式”。
策略迭代的基本框架
根据我们之前看课程学到的内容,我们进行学习的整个思路就是在 Policy Evaluation 和 Policy Imporvement 两个操作间迭代的过程。如下图所示:
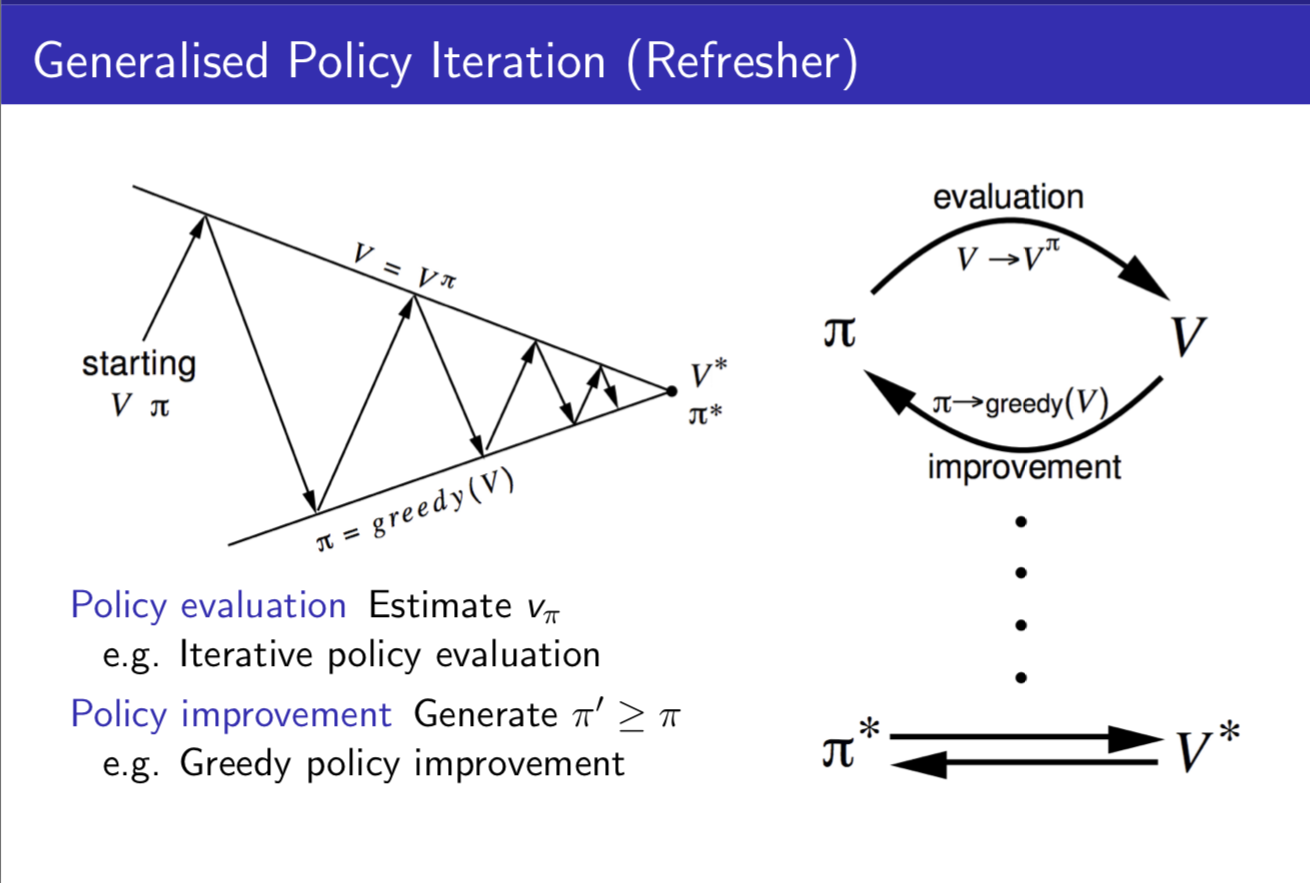
在这个部分我们需要加一个反思,什么是“不基于模型”,“不基于模型”有什么不同。不基于模型会导致以下两个问题:
- 模型未知的时候,我们无法知道当前状态的所有后续状态。这样无法真正“准确”、“理性”地判断当前应该采取什么行为。
- 承接问题 1 ,我们自然而然想到用采样的方式来学习。但是不足的采样会导致得到非最优策略,这样我们需要去尝试一些新的行为。 注:这里小帅哥讲了一个左边的门,还是右边的门的例子,来解释这种情况
Online-Policy Monte-Carlo Control
针对上面的两个问题,给出的一个解决方案如下(注意这种思想同样适用于 TD):
-
针对第一个问题,很直觉的思路就是,对当前策略在所有状态下,产生的所有行为的结果进行采样,并以此为基准更新 $Q(s,a)$ ,其中 $Q$ 为状态对应下的行为的价值,用于代替原有设定中状态的价值。其中更新方法为贪心算法。
\[\pi ' (s) =argmax_{a \in A}\ Q(s,a)\] -
而针对第二个问题的解决问题就有点类似 Multi-armed Bandit 问题,核心在于如何平和 Explore 和 Exploit 的比例。 于是很直觉的思路就是,给他们两个分别以 $\epsilon$ 和 $1 - \epsilon$ 的概率来让两者都能被坚固。其中 $\epsilon$ 代表探索(exploration),即在所有可能的行为中进行选择。而另一个则代表利用(Exploitation),即选取已有的最好的行为。
\[\pi(a|s) = \left\{ \begin{array}{rcl} \epsilon / m + 1 - \epsilon & if & a^{*} = argmax_{a \in A}\ Q(s,a) \\ \epsilon /m & &otherwise \\ \end{array}\right.\]注1:该公式个人也没太看明白
注2:小哥简单的对这样做来优化 q 函数进行了一些简单的推导,证明了最终新的 q 值是递增的
这样子我们把上面的第二个的思想带入回 MC 控制,得到了 MC 控制的全貌图:
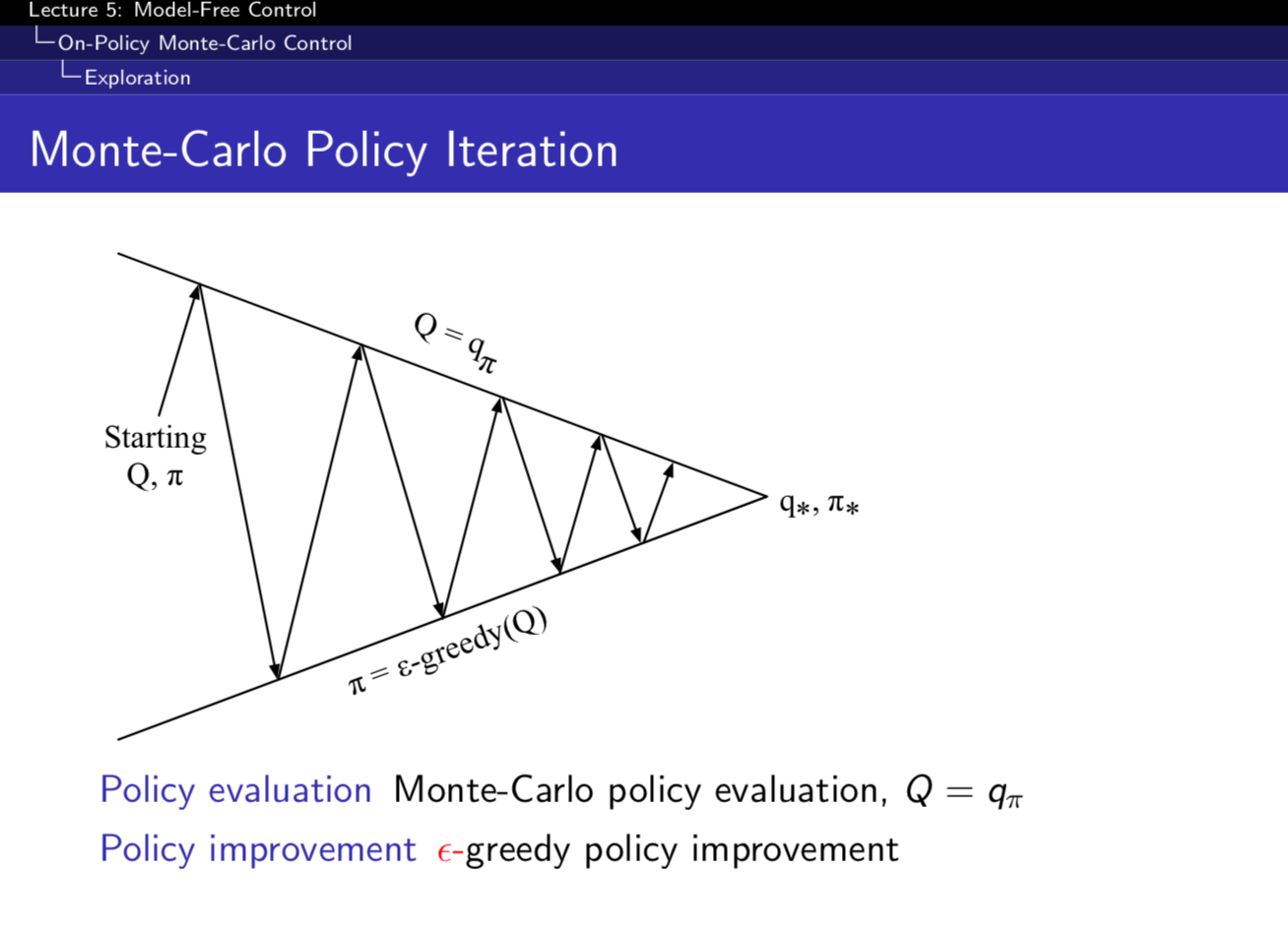
到了这里我们还遇到两个问题:
- 我们不想丢失任何更好的信息和状态
- 我们希望能终止于某一个最优策略。(当前得到的算法中,是可以无限延续的)。在此基础上引入了一个新的概念 GLIE。
GLIE(Greedy in the Limit with Infinite Exploration)
这个概念为,在有限的时间内进行无限可能的探索。具体表现有以下两个特征:
- 对已经经历的状态行为对(state-action pair)会进行无限次的探索
- 随着探索的无限延伸,之前算法中的 $\epsilon$ 回趋向于 0 (这就解决了上面提到的问题)。
具体流程如下:

Online-Policy Temporal-Difference
SARSA
TD 相比 Monte-Carlo 有很多优点,那么我们是不是可以用 TD 代替 MC 呢。而这个思路诞生的算法就是 SARSA。SARSA 的名字的来源就是其训练的过程,如下图所示。
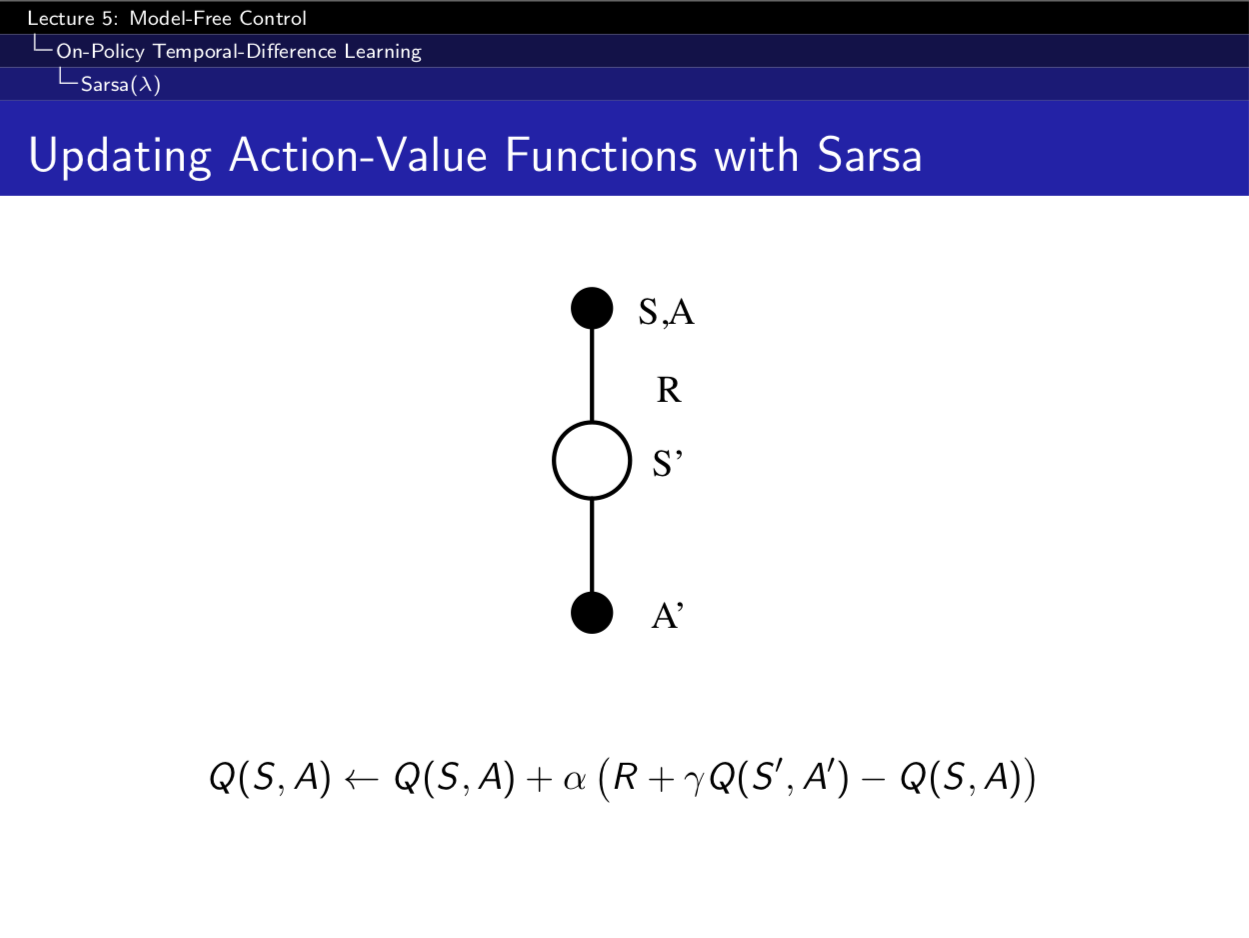

简单的复述下上图的算法流程,首先是第一个 $SA$ ,根据 $Q\ e.g., \epsilon -greedy$,得到一个动作 $A$ 。在执行完动作 $A$ ,之后我们会得到一个即时奖励 $R$,并进入状态 $S’$,之后再根据 $Q$,得到动作 $A’~$。但是这次不执行,根据公式更新 $Q$ 即可。每个步骤汇总起来就是 SARSA。
注:其中 $Q$ 是一个大表存储的,这显然不能用于规模很大的问题
SARSA (λ)
之前的 SARSA 的模型中,只考虑到了未来的一步,那么直觉的来讲,其可以考虑 n 步。于是我们可以得到 n-step SARSA。其给每一步的 $Q$ 的收获都分配一个权重,则会得到 $q^{\lambda}$ 收获。公式如下:
\[q^{\lambda}_t = (1-\lambda)\sum^{\infty}_{n=1} \lambda^{n-1} q_t^{(n)}\]
前向 SARSA 根据某一状态的 $q^{\lambda}$ 收获来更新状态行为对的 $Q$ 值:
\[Q(S_t,A_t) = Q(S_t, A_t) + \alpha(q_t^{\lambda} - Q(S_t,A_t))\]反向 SARSA 反向 SARSA 中,引入了一个新的概念 Eligibility Trace,其针对的是一个状态行为对,体现的是一个结果与某一个状态行为对的因果关系。
\[\begin{split} E_{0}(s,a)&=0 \\ E_{t}(s,a)&= \gamma \lambda E_{t-1}(s,a) + 1(S_t=s, A_t=a) \end{split}\]对 $Q$ 值的更新如下:
\[\begin{split} \delta_t &= R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t) \\ Q(s,a) &= Q(s,a) + \alpha \delta_t E_t(s,a) \end{split}\]整体 SARSA (λ) 如下:

Off-Policy Learning
正如之前提到的,Off-Policy Learning 指的是在遵守一个策略 $\mu (a|s)$ 的同时评估另一个策略 $\pi(a|s)$ 。同时基于 MC 的学习并没有实际应用价值,所以这里就只讨论 TD 下的 Off-Policy Learning。
| 整个的思路就是在遵循策略 $\mu (a | s)$ 的同时评估另一个策略 $\pi(a | s)$ ,所以在具体的数学表示上,就体现在更新 $V(S_t)$ 上面: |
注:Q-Learning 指的就是学习 Q 的算法,并不是一个固定的算法。所以这里就不细说了。详细的参考大佬的博客,或者 PPT 中的算法流程都会有很详细的解释。
参考文献
- 大佬的博客(本次的主要内容就是参考的大佬的博客)
- David Silver 的强化学习课系列