如何表达一个词语的意思
要表达一个词语的意思，首先我们要知道什么是词语的意思呢。
Definition: meaning (Webster dictionary)
- the idea that is represented by a word, phrase, etc.
- the idea that a person wants to express by using words, signs, etc.
- the idea that is expressed in a work of writing, art, etc.
从这个定义中，我们可以看到，一个词语的意思是通过以一个含义和一个符号（词语）进行对应来表达的，有一种 key - value 的意味。
计算机处理词语
这里主要有两个思路，一种称为discrete / symbolic representation，另一种为 distributed representations。而后者是现在主流的思路。
- discrete / symbolic representation
在早期的计算机处理方案是使用分类词典，人工的把不同的单词按照某种关系按层分类，如 NLTK 中可以通过 WordNet 查询熊猫的hypernyms (is-a，上位词)，得到“食肉动物”“动物”之类的上位词。但是这种做法的坏处也是明显的：
- 同义词的意思实际上还是有微妙的差别：adept, expert, good, practiced, proficient, skillful
- 缺少新词，而且不可能做到实时更新
- 需要花大量人力去整理，同时有很强的主观化
- 无法计算准确的词语相似度，因为 one-hot 向量表达的不同词之间的点积只能是 0 / 1。
注：无论是规则学派，还是统计学派，绝大多数NLP学家都将词语作为最小单位。事实上，词语只是词表长度的 one-hot 向量，这是一种 localist representation（一种通过表达词语在语料库中的位置的方式）。在不同的语料库中，词表大小不同，也就是意味着每个 one - hot 向量的长度就不同。试想，Google的 1TB 语料词汇量是1300万，这个向量就大约有 24 维。
- distributed representations
为了表达词语在符号层面上的相似度，我们需要用一种更为合适的方式来编码。在这点上语言学家给我们了启发，J. R. Firth 提出，通过一个单词的上下文可以得到它的意思。他甚至认为，只有你能把单词放到正确的上下文中去，才说明你掌握了它的意义。
”You shall know a word by the company it keeps” ——— From (J. R. Firth 1957: 11)
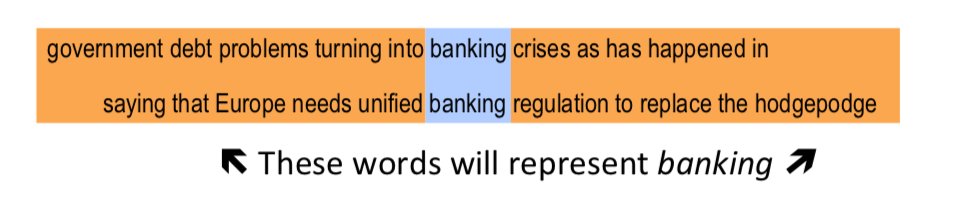
这么做也就引入了另一个变量，即上下文。我们都知道机器学习是基于统计学的，只有更多的数据被引入才能好的提升我们的模型。
神经网络 word embeddings 的基本思路
-
定义一个选定中心词后表达预测正确上下文的某个单词的模型：
\[p(contex|w_1) = ...\] -
定义损失函数
\[J = 1 - p(w_{-t}|w_t)\]其中 $w_{-t}$ 表示 $w_t$ 的上下文。在以后的表示中（负号表达除 XX 之外的集合），若全部预测正确，该函数为 0。
word2vec 的主要思想
Word2vec 顾名思义就是将词用向量来表示，课中提及了如下两种算法和两种高效的训练方式。
两种算法：
-
Skip-grams(SG)：预测上下文
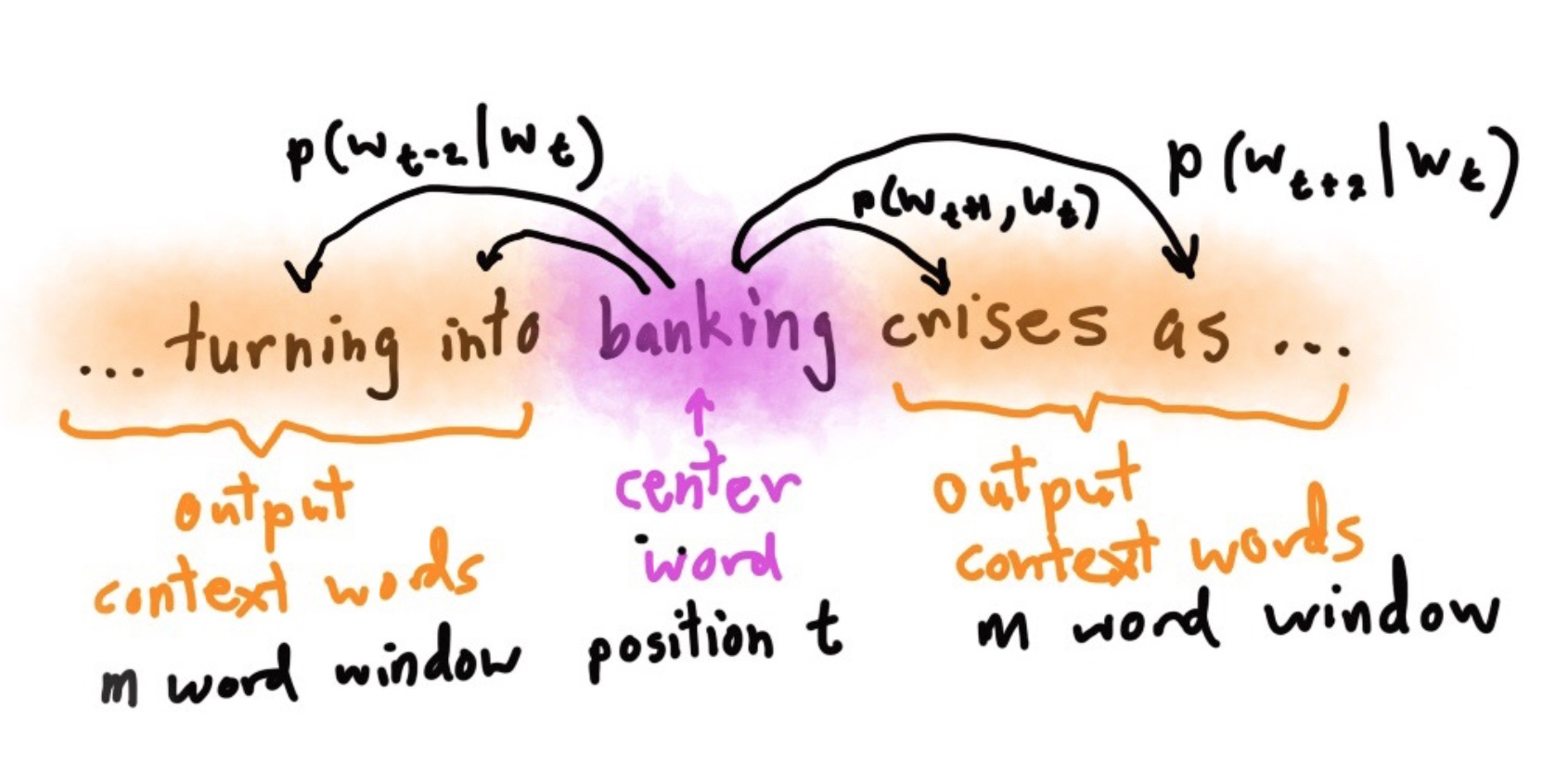注：课程中的算法 - Continuous Bag of Words （CBOW）：预测目标单词 两种稍微高效一点的训练方法：
- Hierarchical softmax
- Negative sampling 注：其他的几个的大佬的博客推导
Word2vec 细节实现
首先可以由定义写出中心词 $w_t$ 对于窗口为 $m$ 的上下文的预测结果，即所有位置的预测结果的乘积：
\[J(\theta) = \prod\limits_{t=1}^{T}\prod\limits_{\substack{-m \leq j \leq m \\ j \neq 0}} log({p(w_{t+j}|w_t)})\]之后，由于乘积的运算非常缓慢，所以使用 $log$ 将其转换为求和的形式：
\[J(\theta) = - \frac{1}{T}\sum\limits_{t=1}^{T}\sum\limits_{\substack{-m \leq j \leq m \\ j \neq 0}} log({p(w_{t+j}|w_t))}\]注：目标函数的术语有好几种，Loss function，cost function,objective function这些都是。对于 softmax 来说，常用的损失函数为交叉熵。
而其中某个上下文的条件概率密度 $p(w_{t+1} |w_t)$，我们使用 softxmax 来得到：
\[p(o|c) = \frac{exp(u_o^T v_c)}{\sum_{w=1}^v exp(u_w^T v_c)}\]注：
其中 o 是输出的上下文词语中的确切某一个，c 是中间的词语。u 是对应的上下文词向量，v 是词向量。
我们用点积代表两个向量的相似程度，越大越相似
Softmax function：是一种从实数空间到概率分布的标准映射方法
Skipgram
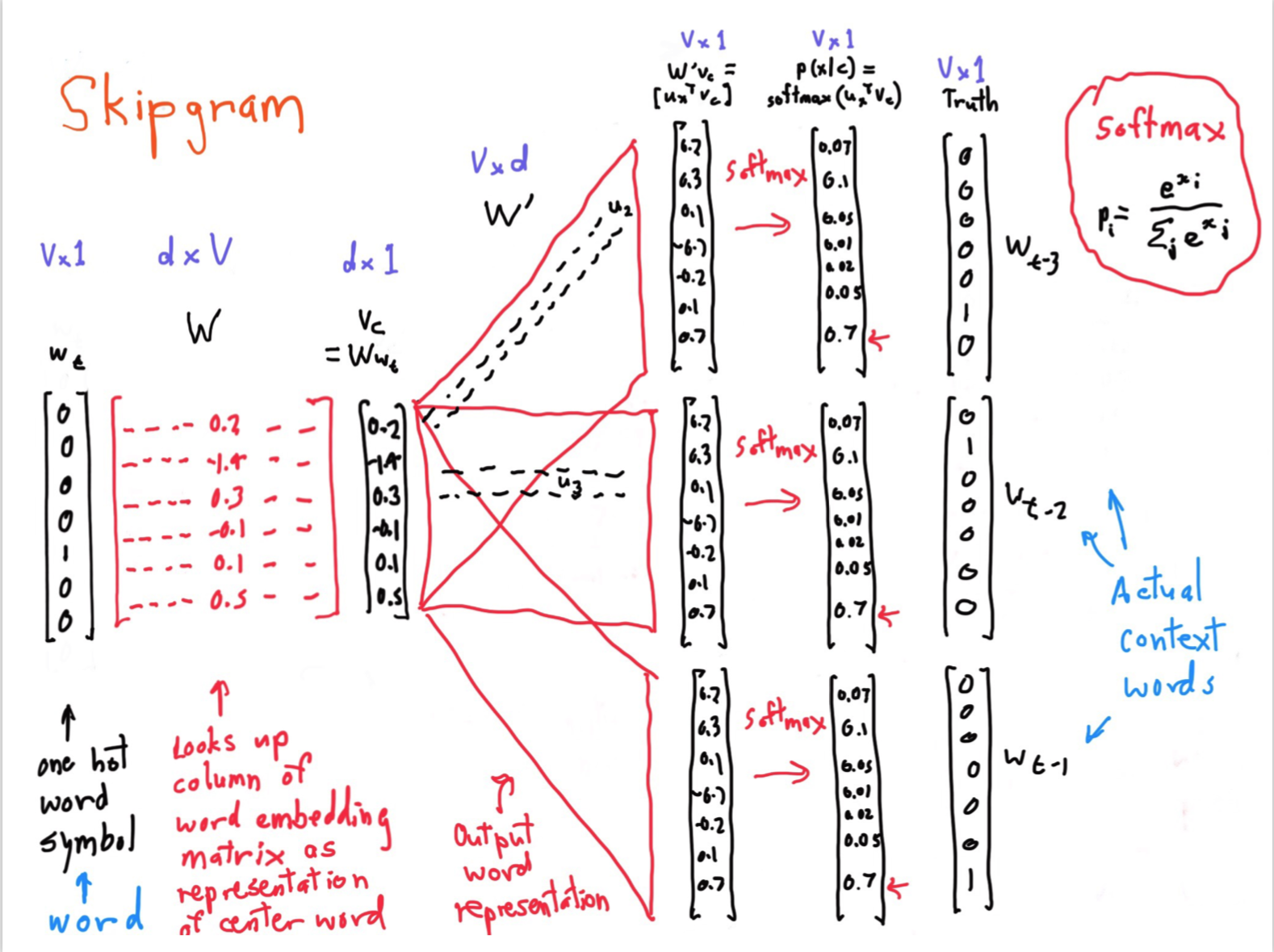这个是课堂中老师使用的 ppt，虽然有点乱，但是解释的还算清楚，但是第一次看很容易晕。以下对一些重点进行解释。
- 第一个 $W$ 指的是词库的每个单词向量
- 第二个 $W’$ 指的是文章的上下文，每一个向量都代表着单词。
- $w_t$ 和 $Truth$ 都是 one-hot 向量，都代表着选中某一个位置
现在来分析整体的过程是什么样子的。
- 首先通过 $w_t·W$ 得到中心词的第一个向量。
- 之后用得到词的向量去和文章中的所有向量点积，即 $v_c·W’$。得到中心词和文中所有词的相似度。
- 通过 softmax 将相似度转成概率。
-
最后通过 $Truth$ 这个one-hot向量，将所有的紧挨着中心词的位置中的概率提出来。
注：这步就是指，我们得到了中心词和周围的所有词的相似度之后，通过one-hot向量将实际中中心词周围的词和中心词的相似度取出来。乘在一起就是之前说的损失函数。
-
进行梯度下降算法
注：
- 这一步就是通过调整 $W$ 和 $W’$ 的值，最终得到词库的单词向量 $W$ 和基于上下文的词库的向量 $W’$。
- 对于表示一个词的两个向量，我们通过求和或者拼接来使用
课堂有意思的参考
Christopher Manning 的 BabyMath
课堂其他有趣的点
-
Christopher Manning 提到的矩阵求导公式：
\[\frac{\partial x^T a}{\partial x} = \frac{\partial a^T x}{\partial x} = a\] - BP就是链式法则（Chain Rule）！
- 神经网络喜欢嘈杂的算法，这可能是SGD成功的另一原因。