知识前置
这个章节的机器学习,其实更像是一种概率论的学习,同时这也是机器学习和数据分析中非常重要的一环。如果学习遇到了困难非常推荐参考张宇考研概率论部分的内容。同时这一章的算法,也是在文本分类中使用的比较多的。
名词解释:
- 先验概率:$P(A)$
- 条件概率:$P(A|B)$
- 后验概率:$P(B|A)$
- 全概率:$P(B) = \sum_{i=1}^n P(A_i)*P(B|A_i)$
- 贝叶斯公式:$P(A|B) = \frac{P(A)P(B|A)}{\sum_{i=1}^n P(B|A_i)P(A_i)}$
概率分布:
- 高斯分布:简单的来说它的分布呈现的是正态分布的样子。参考链接
- 伯努利分布:伯努利分布是0-1分布,简单的来说就是那种仍硬币的概率分布。参考链接
- 多项式分布:是伯努利分布的推广,不再是只有两种情况,有多种情况的概率分布。参考链接
贝叶斯算法的核心思想:
找出在特征出现时,各个标签出现的概率,选择概率最大的作为其分类。
贝叶斯算法
朴素贝叶斯
我们来“望文生义”的理解这个算法,贝叶斯指的就是上面的贝叶斯公式,而朴素则指的是“特征之间是独立的”这个朴素假设。
假设有给定样本X,其特征向量为$(x_1,x_2,…,x_m)$,同时类别为$y$。算法中使用公式2.1表达在当前特征下将类别y预测正确的概率。由于特征属性之间是假定独立的,所以$P(x_1,x_2,…x_m)$是可以直接拆开的,故根据这个特性优化,得到公式2.2。由于样本给定的情况下,$P(x_1,x_2,…,x_m)$的值不变,故研究概率最大的问题只需要研究公式2.2等号右侧上面的部分,最终写出预测函数公式2.3。
\[P(y\|x_1,x_2,...,x_m) = \frac{P(y)P(x_1,x_2,...,x_m\|y)}{P(x_1,x_2,...,x_m)}\ \ \ 公式2.1\] \[P(y\|x_1,x_2,...,x_m) = \frac{P(y)\prod_{i=1}^m P(x_i\|y)}{P(x_1,x_2,...,x_m)}\ \ \ 公式2.2\] \[\hat{y} = arg\ max_y P(y) \prod_{i=1}^m P(x_i\|y) \ \ \ 公式2.3\]到这里,算法的流程就很显而易见了,和softmax算法类似,让预测正确的概率最大即可,具体计算流程如下:
设$x = {a_1,a_2,…a_m}$为带分类项,其中a为x的一个特征属性,类别集合$C={y_1,y_2,…y_n}$
- 分别计算所有的$P(y_i|x)$,使用上述公式2.3
- 选择$P(y_i|x)$最大的$y_i$作为x的类型
其他朴素贝叶斯
高斯朴素贝叶斯
在上述贝叶斯算法中的特征是离散的,那么考虑特征属虚连续值时,且分布服从高斯分布的情况下。用高斯公式(公式3.1)代替原来计算概率的公式。那么根据训练集中,对应的类别下的属性的均值和标准差,对比待分类数据中的特征项划分的各个均值和标准差,即可得到预测类型。
\[p(x_k\|y_k) = g(x_k,\eta_{y_k},\sigma_{y_k}) = \frac{1}{\sqrt{2 \pi}\sigma}e^{-\frac{(x-\eta_{y_k})^2}{2\sigma_{y_k}^2}}\ \ \ 公式3.1\]伯努利朴素贝叶斯
特征值的取值是布尔型的,是有true和false,符合伯努利分布,那么其$P(x_i|y_k)$的表达式如下公式3.3。
\[P(x_i\|y_k)= P(x_i = 1 \| y_k)*x_i + (1-P(x_i=1\|y_k))(1-x_k)\ \ \ 公式3.2\]注:这意味着没有某个特征也可以是一个特征,其中公式3.2其实是把两个不同条件的概率公式融合在一起了,这种方法也在逻辑回归中使用过
多项式朴素贝叶斯
特征属性分布服从多项分布时,得到如下公式3.3,公式的来源简单的来说就是已知盒子中红球和所有球的总个数,求从盒中摸到红球的概率差不多。 其中$N_{y_k x_i} $为类别$y_k$下,特征$x_i$出现的次数,$N_{y_k}$指的是类别$y_k$下,所有特征出现的次数。
\[P(x_i\|y_k) = \frac{N_{y_k x_i} + \alpha}{N_{y_k} + \alpha n}\]注:待预测样本中的特征xi在训练时可能没有出现,如果没有出现,则$N_{y_k x_i} $ 值为0,如果直接拿来计算该样本属于某个分类的概率,结果都将是0。所以在分子中加入α,在分母中加入αn可以解决这个问题。
贝叶斯网络
由于之前朴素贝叶斯,前提条件是假定特征值之间没有关系,这显然是不现实的而贝叶斯网络正是解决这个问题的。其关键方法是图模型,我们构建一个图模型,把具有因果联系的各个变量联系在一起。贝叶斯网络的有向无换图中的节点表示随机变量,连接节点的箭头表示因果关系。
简单的来说贝叶斯网络就是模拟人的认知思维推理模式的,用一组条件概率以及有向无换图对不确定关系推理关系建模。
而这种方式在深度学习之前是很受欢迎的,它和之后的隐马尔可夫被使用作为提取特征的工具,而现在渐渐的过度到了深度学习。
贝叶斯网络工作原理
首先贝叶斯网络的实质就是建立一个有向无环图,其中方向代表因果关系。仔细思考一下,为什么是有向无环图,是因为如果是有环的话,就会有节点是自己依赖于自己,显然这样是有问题的。
具体贝叶斯工作的核心原理可以理解为,根据人已知的经验或者其他手段,规定一些完全没有依赖于其他事件的事件发生的概率,随后根据制作的贝叶斯网络(因果关系图)推算出不同事件发生的概率。这个过程有点像是在做一个概率论的期末考试题,已知A,B,C的概率和ABCD之间转换的关系,问在发生了BC条件下,发生D的概率。大体就是这样一种感觉。
事例如下图:
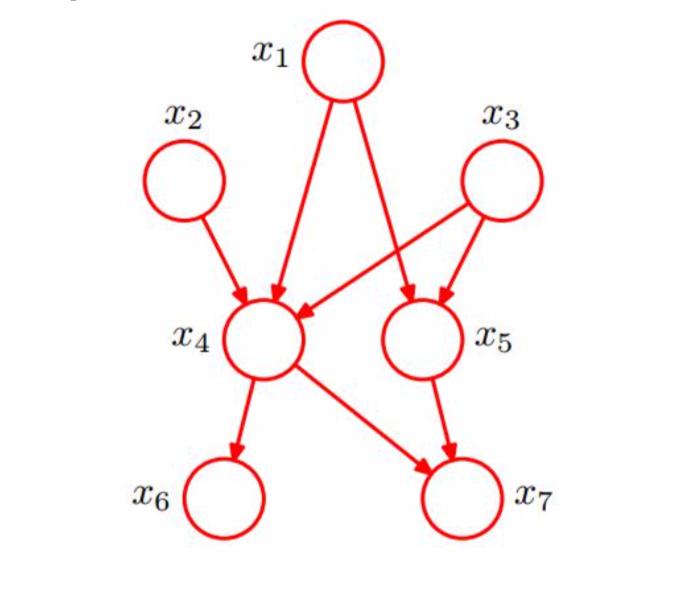
其中$x_1,x_2,x_3$独立,则$x_6,x_7$独立,$x_1,x_2,x_3,…,x_7$的联合概率分布如下:
\[p(x_1,x_2,...,x_7) = p(x_1)p(x_2)p(x_3)p(x_4\|x_1,x_2,x_3)p(x_5\|x_1,x_3)p(x_6\|x_4)p(x_7\|x_4,X_5)\]实际上这部分的概率计算,其实就是根据初始条件和转移方式,求的目标的概率这样的过程。和之前常用的最大似然估计算法对比,贝叶斯的这一系列算法考虑了先验概率,而最大似然估计算法没有,在最大似然估计算法中其实相当于默认了先验概率是相同的。
注:最大后验概率MAP其实可以看作是贝叶斯算法和最大似然估计算法结合的应用